* 压力*

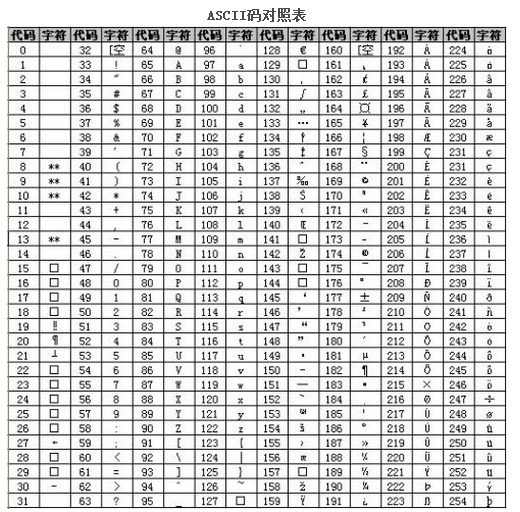
//判断是否是小写字母   大写字母   数字字符   字母字符
//        islower(x) isupper(x) isdigit(x) isalpha(a)
//返回一个bool值
//  转大写     转小写
//toupper(x) tolower(x)
//ASCII码转字符 char()  char(97) =='a'
//字符转ASCII码 int()   int('a') ==971
//字符转int stroi(s);
//int转字符 to_string(n);

//跟整数相关的库函数:
//	绝对值函数	abs()	abs(-5)==5
//	最大值	max(x,y)	max(1,2)==2 max('a','z')==z
//	最小值	min(x,y)	min(1,2)==1
//	交换	swap(x,y)	a=3,b=4;swap(a,b);a=4,b=3
//	取整	int()	int(1.23)==1
//	指数函数	pow(x,y)	pow(2,3)=8
//	随机数	rand()	产生0到RAND-MAX之间的随机整数

//跟实数相关的函数
//向下取整	floor(x) floor(3.14)==3
//向上取整	ceil(x) ceil(3.14)==4
//四舍五入	round(x)	round(5.5)==6
//取整		trunc(x)	trunc(5.5)==5
//对数函数	log底数(x)	log2(8)==3
//平方根值函数	sqrt(x)	sqrt(25)==5
//取绝对值	fabs(x)	fabs(-1.2)==1.2

//scanf函数的格式控制符
//格式控制符	说 明
//%d	用于输入十进制整数
//%o	用于输入八进制整数
//%x	用于输入十六进制整数X  abcdef
//%c	用于输入单个字符
//%s	用于输入字符串
//%f	用于输入实数
//scanf函数的附加格式说明符
//附加格式	说 明
//l	用于超长整型数（%lld、%llo、%llx）或者double型实数(%lf)、long double(%Lf)
//h	用于短整型数（%hd、%ho、%hx）

//格式化输出函数printf
//printf函数的功能是格式化输出任意数据列表，格式是
//printf("格式控制符",输出变量)
//printf函数的格式符
//格式符	说 明
//%d	有符号十进制输出
//%x	无符号十六进制输出
//%o	无符号八进制输出
//%c	输出一个字符
//%s	输出字符串
//%f	小数形式输出单、双精度（隐含输出6位小数）
//d（整型）和f（浮点）格式符
//参 数	说 明
//%md	输出m位（大于m时按照实际长度输出），相当于setw
//%*d	宽度值，例如printf("%*d",y,x)y表示宽度
//%-md	同上。但左对齐
//%md	输出宽度为m的长整型数据、超长整型数据
//%0md	位数不足m时补0
//%lf	小数形式输出，隐含输出6位
//%.mlf	小数形式输出，指定输出m位,当变量为double
//%.mLf	小数形式输出，指定输出m位,当变量为long double
//%.*lf	printf("0.*lf",y,x)表示输出x时，会保留y位小数

// bitset<N> varm(n):
        //类型 N表示需要几位 varm变量名 n表示要转换的数
        //函数名称	作用
        //any()	    检查这些位(bit)中至少有一位或多位被设为1，返回true 或false
        //none()	如果bitset对象全是0就返回ture
        //count()	返回被设置为1的个数
        //set()	    来操作设置某个位数
        //set()     默认全部设置为1
        //set(index , value)
        //test()	测试某个数是否为1
        //test(2)
        //reset()	来操作设置某个位数为0
        //flip()	翻转整个bitset对象

// &    按位与	两个位都是1，结果才是1	9(00001001)&5(00000101)=1(00000001)
// ｜    按位或	两个位只要有一个位是1，结果就是1	9(00001001)|5(00000101)=13(00001101)
// ^  	按位异或	相同为0，不同为1	1^1=0，0^0=0，1^0=1，0^1=1。
// ~	    把运算数所对应的二进制数	把运算数所对应的二进制数按位取反	~7(00000111)=(11111000)
// <<	左移	把运算数的二进制数左移若干位，高位丢弃，低位补0	a<<4，二进制数左移4位
// >>	右移	把运算数的二进制数右移若干位，高位补0，低位丢弃	a>>2，二进制数右移2位

//__builtin_ffs(x)	返回x中最后一个为1的位是从后向前的第几位
//__builtin_popcount(x)	x中1的个数
//__builtin_ctz(x)	x末尾0的个数
//__builtin_clz(x)	x前导0的个数
//__builtin_parity(x)	x中1的奇偶性，1有偶数个返回0，否则返回1

//vector<int> v;	创建空vector
//    v.push_back(x)	向尾部增加一个元素x
//    v[i]	访问i位置元素
//    v.pop_back()	删除vector中最后一个元素
//    v.size()	返回vector中元素的个数
//    v.clear()	清空vector中所有元素
//    v.empty()	判断vector是否为空
//    迭代器
//    v.begin()	返回vector头指针，指向第一个元素
//    v.end()	返回vector尾指针，指向最后一个元素+1的位置
//    v.erase(v.begin()+i)	删除第i位位置元素
//    v.insert(pos,x)	向pos地址指向的元素前增加一个元素x
//vector<int>::iterator it  it迭代器变量

//lower_bound(a,a+n,4);//查找到第一个不小于这个值的地址
//upper_bound(a,a+n,4);//查找到第一个大于这个值的地址
//next_permutation(a,a+n)//下一个全排列
//prev_permutation(a,a+n)//上一个全排列

//greater<int>()    从大到小
//less<int>()       从小到大
//unique 去重
//next_permutation 会尝试将序列重新排列成大于当前排列的最小排列

Visual Studio Cod

//string s1,s2,s3
    //s1.find(s2)     在字符串s1中找到s2,找到了返回匹配的字符串的首个下标
    //                没找到返回一个常数string::npos
    //s1.substr(i,n)  在下标为i处开始截取n个字符
    //s1.erase(i,n)   在下标为i处开始删除n个字符  
    //s1.insert(i,s3) 在下标为i处开始插入字符串s3
    //reverse()       翻转字符串
    string a="123456789",b="123";
    // if(a.find(b)!=string::npos){
    //     cout<<a.find(b);
    // }else{
    //     cout<<"no";
    // }
    cout<<a.substr(0,7)<<endl;
    cout<<a<<endl;
    a.erase(0,9);
    cout<<a<<endl;
    a.insert(0,"1234567");
    cout<<a<<endl;
    a.insert(1,"x");
    cout<<a<<endl;
    a.insert(8,"x");
    cout<<a<<endl;
    reverse(a.begin(),a.end());
    cout<<a;

//链表
//单向：
#include<bits/stdc++.h>
using namespace std;
const int N=100;
struct node{
    int id,nextid;
}nodes[N];

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        nodes[i].id=i;
        nodes[i].nextid=i+1;
    }
    nodes[n].nextid=1;
    int now=1,prew=n;
    while((n--)>1){
        for(int i=1;i<m;i++){
            prew=now;
            now=nodes[now].nextid;
        }
        cout<<nodes[now].id<<" ";
        nodes[prew].nextid=nodes[now].nextid;
        now=nodes[prew].nextid;
    }
    cout<<nodes[now].id;
    return 0;
}
//双向：
#include<bits/stdc++.h>
using namespace std;
const int N=100;
struct node{
    int id,nextid,preid;
}nodes[N];

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        nodes[i].id=i;
        nodes[i].nextid=i+1;
        nodes[i].preid=i-1;
    }
    nodes[n].nextid=1;
    nodes[1].preid=n;
    int now=1;
    while((n--)>1){
        for(int i=1;i<m;i++){
            now=nodes[now].nextid;
        }
        cout<<nodes[now].id<<" ";
        int prew=nodes[now].preid,next=nodes[now].nextid;
        nodes[prew].nextid=next;
        nodes[next].preid=prew;
        now=next;
    }
    cout<<nodes[now].id;
    return 0;
}

//10转n
#include<bits/stdc++.h>
using namespace std;
char f1(int n){
    if(n>9){
        return n+'A'-10;
    }else{
        return n+'0';
    }
}
string f(int s,int n){
    string sum="";
    while(s>=1){
        sum+=f1(s%n);
        s/=n;
    }
    return sum;
}
int main()
{
    int s;
    int n;
    cin>>s>>n;
    if(s<0){
        s=abs(s);
        string a;
        a=f(s,n);
        reverse(a.begin(),a.end());
        cout<<'-';
        cout<<a;
    }else{
        string a;
        a=f(s,n);
        reverse(a.begin(),a.end());
        cout<<a;
    }
    return 0;
}

//n转10
#include<bits/stdc++.h>
using namespace std;
int f1(int n){
    if(isdigit(n)){
        return n-'0';
    }else if(isalpha(n)){
        return toupper(n)-'A'+10;
    }else{
        return 0;
    }
}
int f(string s,int n){
    int sum=0;
    int len=s.size();
    for(int i=0;i<len;i++){
        sum=sum*n+f1(s[i]);
    }
    return sum;

}
int main()
{
    string s;
    int n;
    cin>>s>>n;
    cout<<f(s,n);
    return 0;
}

#include<stack>
#include<vector>
#include<deque>
#include<cstdio>
#include<list>
#include<cmath>
#include<string.h>

//判断素数
bool is_prime(int n){
    if(n<2){
        return false;
    }
    for(int i=2;i*i<n;i++){
        if(n%i==0)return false;
    }
    return true;
}
//埃式筛选法
void as_prime(bool a[]){
    a[0]=a[1]=1;
    for(int i=2;i*i<n;i++){
        if(!a[i]){
            for(int j=i*i;j<=n;j+=i){
                a[j]=1;
            }
        }
    }
}
//欧拉
void ol_prime(){
    for(int i=2;i<m;i++){
        if(!prime[i]){
            a[n++]=i;
        }
        for(int j=0;j<n && i*a[j]<=m;j++){
            prime[i*a[j]]=1;
            if(i%a[j]==0){
                break;
            }
        }
    }
}

int find(int pos){
    if(pos>size||pos<0){
        cout<<
        return -1;
    }else{
        int fd=head;
        for(int i=1;i<=pos;i++){
            fd=nxt[fd];
        }
        return fd;
    }
}
void push_front(int x){
    if(idx>max_size-1){
        cout<<
    }else{
        val[idx]=x;
        nxt[idx]=nxt[head];
        nxt[head]=idx;
        idx++;
        size++;
    }
}
void insert(int x,int pos){
    if(pos>size||pos<=0){
        cout<<
        return -1;
    }else if(idx>max_size-1){
        cout<<
    }else{
        int temp=find(pos-1);
        val[idx]=x;
        nxt[idx]=nxt[temp];
        nxt[temp]=idx;
        idx++;
        size++;
    }
}
void push_back(int x){
    if(idx>max_size-1){
        cout<<
    }else{
        int temp=head;
        while(nxt[temp]!=-1){
            temp=nxt[temp];
        }
        val[idx]=x;
        nxt[idx]=idx;
        nxt[idx]=-1;
        idx++;
        size++;
    }
}
void pop_front(){
    if(size==0){
        cout<<
    }else{
        nxt[head]=nxt[nxt[head]];
        size--;
    }
}
void pop_back(){
    if(size==0){
        cout<<
    }else{
        int temp=head;
        while(nxt[nxt[head]]!=-1){
            temp=nxt[temp];
        }
        nxt[head]=-1;
        size--;
    }
}
void erase(int pos){
    if(size==0){
        cout<<
    }else{
        int temp=find(pos-1);
        nxt[temp]=nxt[nxt[temp]];
        size--;
    }
}
void modify(int pos,int x){
    if(pos>size||pos<=0){
        cout<<;
    }else{
        val[find(pos)]=x;
    }
}

//二分查找：
#include<bits/stdc++.h>
using namespace std;
int binary_seach(int a[],int L,int R,int key){
    int ret=-1;
    while(L<=R){
        int mid=(L+R)/2;
        if(a[mid]==key){
            ret=mid;
            break;
        }else if(a[mid]<key){
            L=mid+1;
        }else{
            R=mid-1;
        }
    }
    return ret;
}
int main()
{
    int a[10]={1,2,3,5,7,8,9,78,91,250};
    cout<<binary_seach(a,0,9,78);
    return 0;
}

二叉树的性质：

1、若节点数为n，则边的数量为n-1

2、叶子节点和度为2节点的关系：n0=n2+1

3、二叉树第k层最多有2^k-1个节点

4、二叉树深度为h，则二叉树最多有2^h+1-1个节点

满二叉树的性质：

1、满二叉树第k层有2^k-1个节点

2、层数为k的满二叉树总共的节点树量一定有2^k-1个，叶子节点树为2^k-1。

3、满二叉树中不存在度为1的节点，每一个分支节点中都有两棵深度相同的子树，且叶子节点都在最底层

4、具有n个节点的满二叉树的层数为log₂(n+1)

完全二叉树的性质：

1、假定根节点从1开始编号，满二叉树的节点有父节点，则其父节点的编号为i/2；若有左子节点，则座子节点的编号为2* i；若有右子节点，则右子节点的编号为2* i+1。

2、如果2* i+1>n(总节点的个数)，则节点i肯定没有左子节点(为叶子节点)，否则左孩子的编号是2* i。

3、如果2* i+1>n，则节点i肯定没有右子节点；否则右子节点的编号是2 *i+1。

4、n个节点的完全二叉树的深度为floor(log₂(n))。