问题描述

现有一棵由 $n$ 个节点组成的无向树，节点编号从 $0$ 到 $n - 1$，共有 $n - 1$ 条边。

给你一个二维整数数组 $edges$，长度为 $n - 1$，其中 $edges[i] = [a_i, b_i]$ 表示树中节点 $a_i$ 和 $b_i$ 之间存在一条边。另给你一个整数数组 $restricted$ 表示 受限 节点。

在不访问受限节点的前提下，返回你可以从节点 $0$ 到达的 最多 节点数目。

注意：节点 $0$ 不会 标记为受限节点。

格式

输入

第一行一个整数 $n$，表示节点数量； 接下来 $n - 1$ 行，每行两个整数 $a, b$，表示一条无向边； 接下来一行一个整数 $k$，表示受限节点数量； 最后一行 $k$ 个整数，表示受限节点的编号。

输出

输出一个整数，表示从节点 $0$ 出发，在不访问任何受限节点的前提下，可以访问的最多节点数目。

样例1

7
0 1
1 2
3 1
4 0
0 5
5 6
2
4 5

4

样例一说明

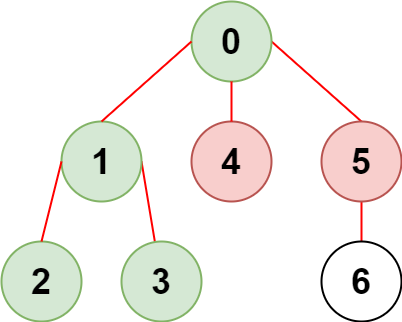
从节点 $0$ 出发，可访问节点为 $0, 1, 2, 3$，由于节点 $4$ 和 $5$ 是受限节点，不能访问，最多访问 $4$ 个节点。

样例2

7
0 1
0 2
0 5
0 4
3 2
6 5
3
4 2 1

3

样例二说明

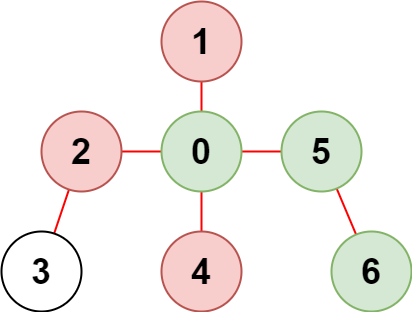
虽然 $4$ 和 $5$ 是受限节点，但不影响访问其它节点，因此可以访问 $0, 1, 2, 3, 6$ 共 $5$ 个节点。

提示

$2 \leq n \leq 10^5$

$edges.length == n - 1$

$edges[i].length == 2$

$0 \leq a_i, b_i < n$

$a_i \neq b_i$

树中不存在重复的边

树是连通图

$1 \leq restricted.length < n$

$restricted$ 中的所有值 互不相同

节点 $0$ 不会出现在 $restricted$ 中